搜索结果: 1-15 共查到“偏微分方程”相关记录1937条 . 查询时间(1.174 秒)
深圳技术大学大数据与互联网学院史诗洁副教授（图）
深圳技术大学大数据与互联网学院 史诗洁 副教授 非线性偏微分方程 生物趋化性
2025/3/21
史诗洁，深圳技术大学大数据与互联网学院副教授，研究方向为非线性偏微分方程，生物趋化性。
深圳技术大学大数据与互联网学院何俊锋副教授（图）
深圳技术大学大数据与互联网学院 何俊锋 副教授 非线性偏微分方程
2025/3/21
何俊锋，副教授，深圳市高层次人才。硕士、博士毕业于首都师范大学应用数学专业。武汉大学-南方科技大学联合培养博士后。主要研究方向为以生态学、物理和化学为背景的非线性偏微分方程。近年来，主持国家自然科学基金青年基金、中国博士后面上项目以及深圳市博士后出站科研项目各一项，教改项目一项；科研项目主要聚焦于反应扩散方程的传播现象，例如种群的传播与入侵以及传染病的传播与消亡等，累计发表SCI学术论文10余篇，...
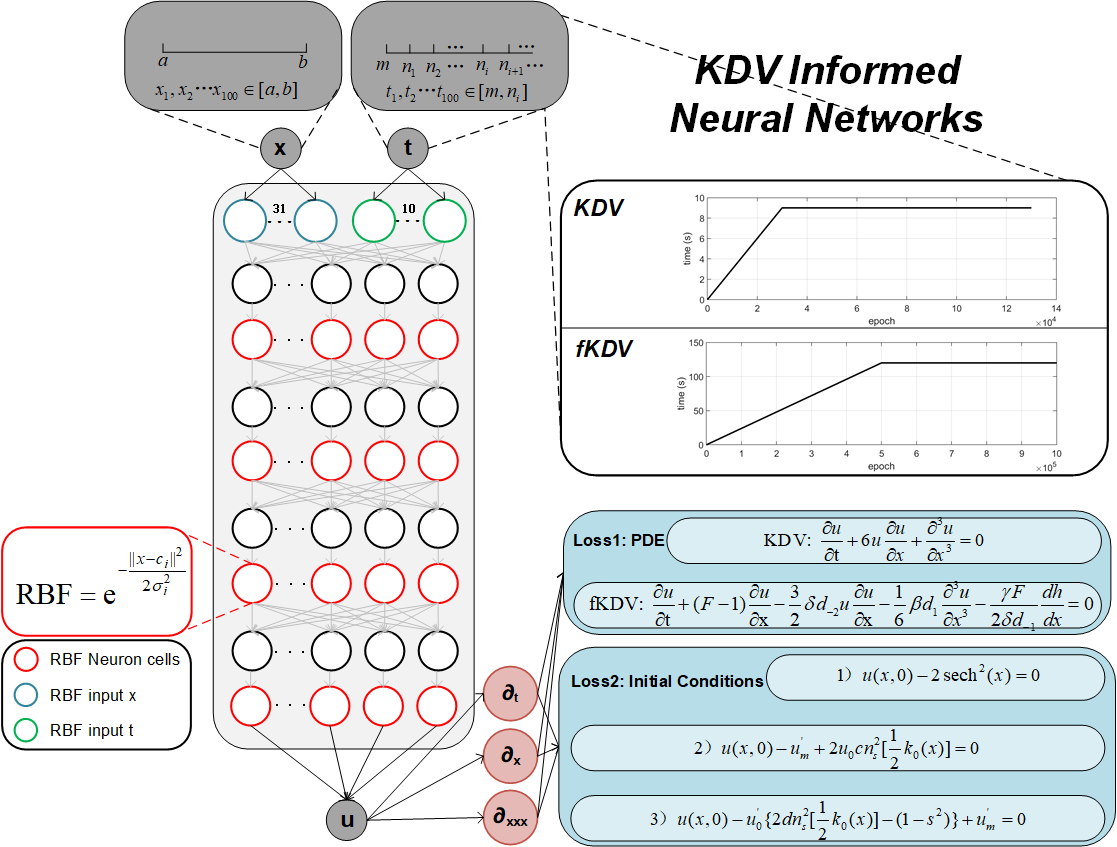
中国科学院海洋所研究团队提出深度学习求解偏微分方程新方法（图）
偏微分方程 信息 神经网络
2025/1/8
2025年1月7日，中国科学院海洋研究所李晓峰研究团队基于深度学习技术，提出了一种高效求解海洋动力学偏微分方程（PDE）的新方法，并成功应用于描述海洋内孤立波的KdV方程组求解。
上海科技大学数学科学研究所岳海天教授与合作者最近的两项研究成果分别发表于《数学年鉴》(Annals of Mathematics) 和《数学新进展》(Inventiones Mathematicae)，相继彻底解决了色散方程领域悬而未决近三十年的两个难题：二维高阶非线性薛定谔方程和三维三阶非线性波方程下的吉布斯测度不变性问题。
中国科学院软件所分布式SMT求解器研究工作获CAV杰出论文奖（图）
系统 结构 非线性算术
2024/9/20
2024年7月25日，中国科学院软件研究所基础软件与系统重点实验室（计算机科学国家重点实验室）的论文Distributed SMT Arithmetic Theories Solving Based on Dynamic Variable－level Partitioning在形式化验证领域国际旗舰会议Computer Aided Verification（CAV 2024）上荣获杰出论文奖（CA...
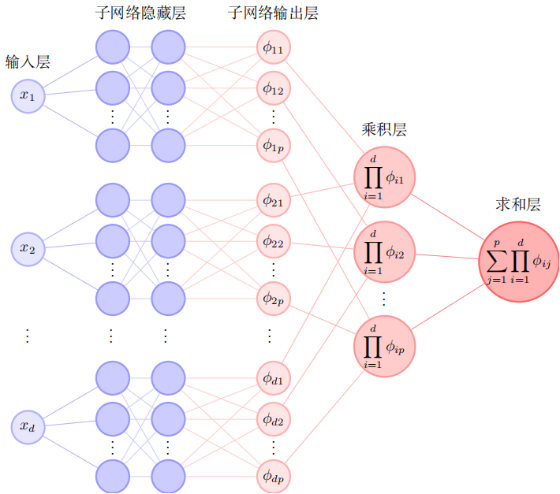
由于“维数灾难”的原因，求解高维偏微分方程一直是数学、物理、化学等学科中具有本质困难的问题。基于深度神经网络的机器学习方法为解决这一问题提供了潜在的可能性，目前已经设计了多种机器学习方法来求解高维偏微分方程。这些方法由于需要进行采样或使用Monte-Carlo方法进行高维积分来计算损失函数，往往导致求解精度远低于经典算法求解低维偏微分方程的精度，实际应用范围也受到了很大的限制。
黄淮学院数学与统计学院吴忠林教授（图）
黄淮学院数学与统计学院 吴忠林 教授 偏微分方程
2024/3/28
吴忠林，男，1972年3月生，教授、博士。1996年7月河南大学数学专业本科毕业。2006年7月河南大学基础数学专业硕士毕业。
上海外国语大学贤达经济人文学院数据科学学院硕士生导师周渊教授（图）
上海外国语大学贤达经济人文学院数据科学学院 硕士生导师 教授 随机控制 数学金融 非线性方程分析 孤立子理论 数据科
2024/3/7
周渊，教授，硕士导师。复旦大学数学系，获理学学士和理学硕士学位，留学美国南佛罗里达大学获数学与应用数学专业博士学位。